在行测数量关系题目中,概率问题是必考题型,可能会有一部分小伙伴认为概率问题不易分析且列式复杂,其实有些概率题目是有简单方法的,今天就给大家分享一个能快速解决这些概率题目的方法——“定位法”。
我们一起看下例题。
【例1】某单位要在会议室开会,会议室有5排共30个座位,每排座位数相同。小李和小赵最先来到会议室,在两人都随机选择座位的情况下,他们恰好坐在同一排的概率:
A.不高于10%
B.高于10%但低于15%
C.高于15%但低于20%
D.高于20%
答案:C
常规解法:会议室有5排共30个座位,每排座位数相同,则每排6个座位。总事件是两人从30个座位中共选取2个座位就坐,
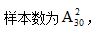
所求事件是两人恰好坐在同一排,则可先从5排中选择一排,再从这一排的6个座位中随机选取2个座位就坐,分步相乘,该样本数为
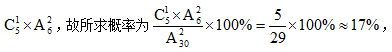
所以选择C选项。
定位法:小李与小赵要选到同一排,他们在选座时无论谁先选都对最终的结果不产生任何影响,同时,无论第一个人选择哪个位置,都不会影响到第二个人选择的等可能性,所以可以利用定位法去求解。假设小李先选,当小李选定一个座位后,小赵还有30-1=29个座位可选,即总样本数为29,和小李在同一排的座位还剩6-1=5个,即所求事件样本数为5,故所求概率为
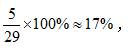
所以选择C选项。
通过对比,定位法比常规解法有明显的优势,列式和计算都非常便捷。因此对于这类问题,建议大家后期使用定位法来求解。
那什么样的题目能够使用定位法呢?
一般情况下当遇到要同时考虑相互联系的元素,如两元素在同一排、分到同一组等等时,即可考虑使用定位法求解概率。
求解时具体的操作是先将其中一个固定,再考虑其他元素的所有等可能情况,从而进行求解。
接下来请大家尝试使用定位法来求解下题。
【例2】某学校举办运动会,有10人报名参加“二人三足”比赛,现将10人随机组成5队,每队2人。那么,小红和小丽恰好被分在同一组的概率是:
答案:A
【解析】小红与小丽在选组时,无论谁先选都对最终的结果不产生任何影响,同时,无论第一个人选择哪一组,都不会影响到第二个人选择的等可能性,所以可以利用定位法去求解。假设小红已确定分队位置,小丽可以选择剩下9个位置,即总事件样本数是9个,要想和小红一队,小丽可选择的只有同队的1个位置,即所求事件的样本数是1个,故所求概率为
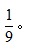


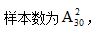 所求事件是两人恰好坐在同一排,则可先从5排中选择一排,再从这一排的6个座位中随机选取2个座位就坐,分步相乘,该样本数为
所求事件是两人恰好坐在同一排,则可先从5排中选择一排,再从这一排的6个座位中随机选取2个座位就坐,分步相乘,该样本数为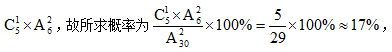 所以选择C选项。
所以选择C选项。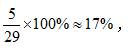 所以选择C选项。
所以选择C选项。