在行测考试中数量关系是必考的部分,主要是为了考察考生理解、把握事物间量化关系和解决数量关系问题的能力,涉及数据的分析、推理、判断、运算等。在考试中比较耗时间,往往会形成有时间就做,没时间就蒙的局面,所以这部分取得高分的考生很少,久而久之对数量关系这部分题目产生畏难情绪,其实有很多题型只要掌握一些答题技巧是可以在短时间内做出来的,例如特值法解题。
一、特值法定义
特值就是利用特殊值解题的一种方法。当题干中某个量未知时,一般情况下,我们很多同学会将未知量设为未知数,例如x,y,z……,而特值法是将未知量设为某个符合题干要求的具体的数值,进而简化计算过程,快速得到正确答案。
二、应用环境
题干中出现“倍数”、“百分数”等文字描述时,所求为比例,且对应量未知。
三、小测验
【例1】一项工程,甲单独做要10天,乙单独做要15天完成。若甲、乙两人合作,需要多少天?
A.5
B.6
C.7
D.8
答案:B
【解析】方法一:设工程总量为X,则甲的工作效率为
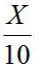
,乙的工作效率为
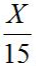
,则甲乙两人合作的效率为
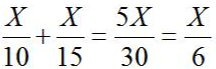
,所求为6天。
方法二:设工程总量为30(10、15的最小公倍数),则甲的工作效率为3,乙的工作效率为2,则甲乙两人合作的效率为3+2=5,所求为
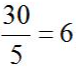
。
两种方法比较而言,第二种方法相对更简单一些,做题也更快捷一些,这就是我们的特值法。
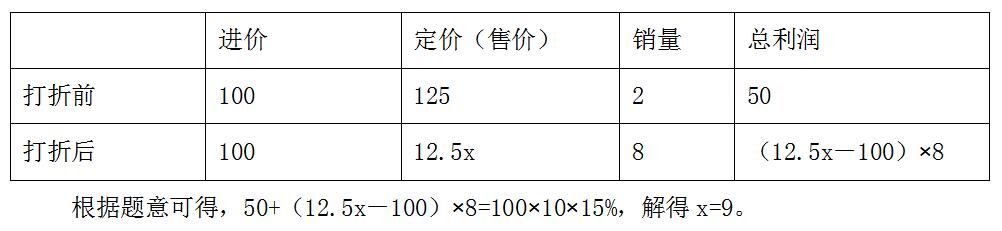
【例2】某商店购进一批篮球,定价为进价的125%,在售出进货量的20%后,商店决定打折促销。篮球全部卖完后,商家在该批篮球上总获利15%,问该商店这次促销价为定价的多少折?
A.8
B.8.5
C.9
D.9.5
答案:C
【解析】设进价为100,销量为10,所以定价为125,打x折后促销价为12.5x。梳理题干信息:
上述两个题型(工程问题、利润问题)都可以运用特值法解题,这种解题方法比利用方程解题快速便捷。运用特值法解题可以省去设未知数解题带来的运算上的麻烦,只要我们多加练习,善于总结,可以将特值法运用到更多的题型中去,起到事半功倍的作用。


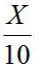 ,乙的工作效率为
,乙的工作效率为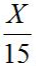 ,则甲乙两人合作的效率为
,则甲乙两人合作的效率为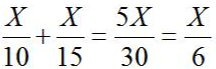 ,所求为6天。
,所求为6天。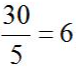 。
。